
A large number of vision chips require processing of information within a neighborhood. Resistive networks have been known as a method of providing local interaction between cells with minimum requirement in terms of space and interconnection. Although general network theories are very helpful in understanding the type of functions realizable using resistive networks, it is in general difficult to find a resistive network suitable for a specific problem. There are a number of resistive networks that have been fully analyzed and characterized. The simplest resistive network is the smoothing network shown in Figure 7.26. The circuit can also be regarded as a diffusive network, as in bulk semiconductors. The kernel of this network is an exponential function with the decaying rate depending on the ratio of the R1 and R2. For a spatial impulse voltage input the voltage distribution is given by [Mead 89b]

where
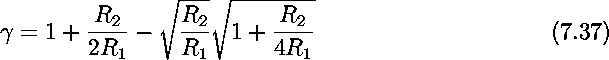
The exponentially decaying smoothing function is not generally used in image processing algorithms, but as it is the simplest network providing spatial smoothing, it has been preferred over more complicated and area consuming networks, for example the Gaussian filtering(See section 2.7), in VLSI implementations. The errors due to device mismatch are usually prevalent and exceed the difference between an exact Gaussian function and an approximated exponential function. Therefore, it is rather unnecessary to use more accurate approximates, unless the specific algorithm heavily relies on the shape of the function, and also device mismatch can be controlled within the desired range.
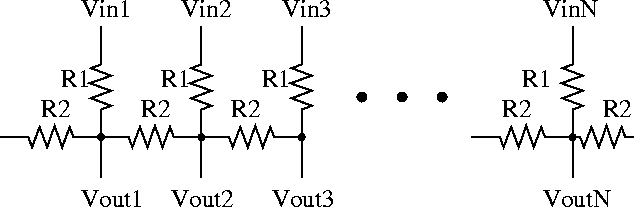
Figure 7.26: Smoothing resistive network.
A more rigorous analysis of resistive networks for early vision processing can be found, for example in [Wyatt 94].