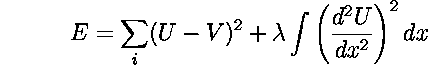
The spatial image Gaussian filter designed by Kobayashi et al. [Kobayashi et al. 95b] uses a hexagonal resistive network. It uses negative resistors implemented using negative impedance converters (NIC) to obtain a better approximation to the Gaussian function, than that obtained using simple resistive networks (an exponentially decaying function similar to charge distribution in bulk semiconductors). The 2D resistor connection is shown in Figure 2.10. In order to get the desired Gaussian characteristic, negative resistances are connected to the second-nearest-neighbors, with four times the value of resistors connecting first-nearest-neighbors. The value ``4'' has been derived from the discretization of the error energy function, E, for optimizing the fitting function U added with a penalty term, described by
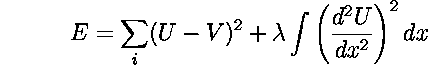
where the first term is the mean square error between the fitting function U and the input V, and the second term is the penalty term. By discretizing this equation and finding its minimum, a relation between the fitting function and the input can be found.
The circuit in Figure 2.11 has been used in the implementation of the NIC elements.
The chip has a 45 
40 array of photodetectors and resistive grid
on a 7.9 9.2mm chip using a 2 
m CMOS process.
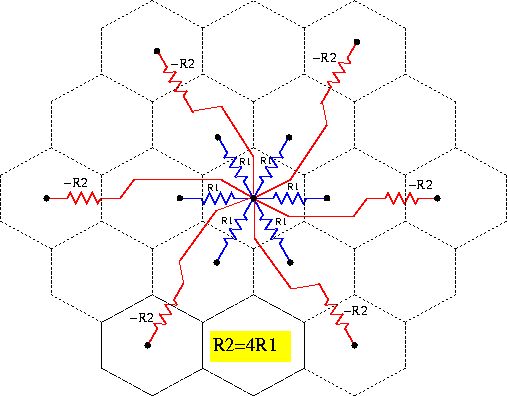
Figure: Kobayashi et al.'s resistive network using negative
impedance converters for implementing a Gaussian filter.
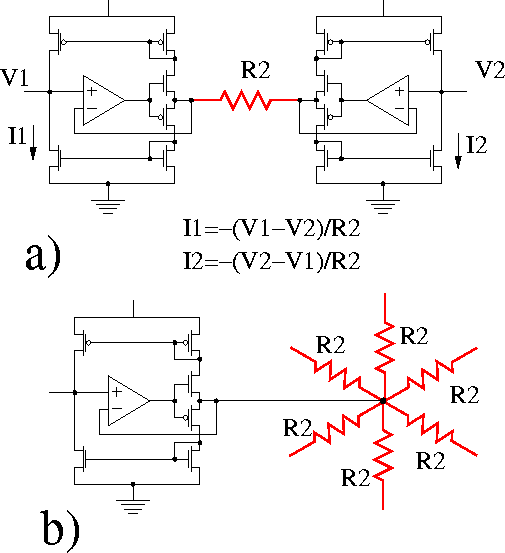
Figure: Negative impedance converter (NIC) used in Kobayashi et al.'s
image Gaussian filter. a) obtaining a negative impedance using a
resistor and two NIC circuits. b) the usage of the NIC circuit in
the chip. One NIC has been used for six resistors.