Spatial Adaptation Models

 

Adaptation the the light level can be achieved by using spatial information and removing the redundant parts of the information. In its simplest and most intuitive form the global spatial average can be used as the common signal among all detectors. Removing the average can be performed by using subtraction or division. The dynamic range will still be limited to a global value. Removing local average instead of the global average can increase the dynamic range by several orders of magnitude. The reason being that each region in the image only adapts to its own average. There has been several models for spatial adaptation which we will review in this section. One may find similarities between the response of the systems based on these models and those from biological retinas. Some of the salient features of the spatial response of biological retina are(See for example [Nabet and Pinter 91]):

• Dynamic range reduction: The output signals of the retina have a much smaller dynamic range than its inputs. Therefore, further processing stages do not need to cope with large dynamic range.
• Edge enhancement: Edges are very important for every image processing task. By enhancing the edges further processing stages will receive more reliable inputs.
• Intensity dependent spatial response: At low light levels, a biological retina acts as a smoothing filter, and at high intensities it performs as a spatial band-pass filter. Also as the light level decreases the span of the spatial processing widens.

These properties have been depicted in Figure 7.42. Now let us review the models.

  
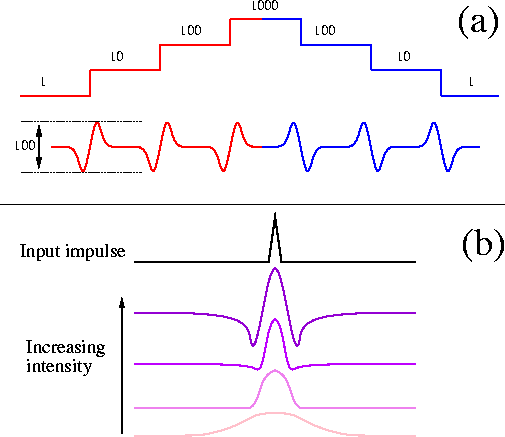
Figure 7.42: Properties of the retina. a) the dynamic range reduction and edge enhancement features. The numbers are just as indicators of the signal levels. b) Intensity dependent response.

1. Subtraction from local average
   In this method the local average is subtracted from the signal in each cell. Sometimes, two local averages with different spatial distribution are subtracted from each other. This method has two disadvantages. Firstly, the signal will be centered around ``zero'', and the signal variation will depend on the local average. For example, if the average current is about 1nA the signal variation will be around this value. Secondly, this method cannot reproduce the intensity dependent response. Due to its intuitive nature this method has been used in many VLSI implementations of the retina [Mead and Mahowald 88, Bair and Koch 91a, Wu and Chiu 95].
2. Division by local average
   In this method the signal from one cell is divided by the local average. One main advantage of this method over subtraction is that the output is now centered around ``one''. Therefore, the output can now be normalized to a desired value. In subtraction method, if an offset (for example 100nA) is added to move the center from ``zero'', small values may get lost. Another advantage of this method is its multiplicative noise cancellation (MNC) feature. By dividing the signal to the local average, AC noise from artificial light source, which reflect from the surface of objects (and hence have a multiplicative nature), can be reduced to a small fraction. In fact this method was first introduced for this purpose [Moini et al. 95a, Moini et al. 97b]. It has been used as a pre-processor in a motion detection chip to reduce the effect of AC light sources [Moini et al. 97b, Moini et al. 95b].

   This method also cannot reproduce the intensity dependent behavior.

3. Surface reconstruction from noisy data
   This model has originally been developed as a way for reducing the noise and recovering the signal from noisy data. Using the regularization theory, one can find the solution to this problem using the biharmonic equation (See section 2.6). The VLSI implementation of this model can produce a normalized output, and demonstrates the dynamic range improvement and edge enhancement features. Although an intensity dependence response has been reported using the implemented circuits, the change of the response is opposite the change in biological retina, i.e. at higher light levels the spatial span of the impulse response becomes wider [Boahen and Andreou 92, Andreou and Boahen 94b].

   The theoretical model also does not originally account for intensity dependent characteristics, but it can be modified to include this feature too.

4. Linear lateral inhibition
   Linear lateral inhibition is a simple form of lateral inhibition, where the signal in one cell is subtracted from fractions of the neighboring cells. This model can demonstrate the edge enhancement and dynamic range improvement features. However, it still cannot reproduce the intensity dependent behavior. This method has been used in the implementation of a few shunting inhibition vision chips [Wolpert and Micheli-Tzanakou 93].
5. Multiplicative lateral inhibition (Shunting inhibition)
   In shunting inhibition (SI) a proportion of the output signals of each cell and its neighbors are subtracted from the signal in each channel (See sections 2.19 and  3.27). This model has in fact been developed to model the behavior of the biological retina. It has demonstrated all properties of the biological retina. Several vision chips have been designed based on shunting inhibition [Darling and Dietze 93, Moini et al. 97a].

It is now clear that many VLSI implementations of the retina have deficiencies, in the context of replicating the function of the retina; and only shunting inhibition can be regarded as the closest model for replicating the functionality of the retina.

However, in the context of providing a vision chip which can improve the dynamic range, enhance the edges, and yet be VLSI friendly the ``division by average'' and the model based on biharmonic equation can also be considered as viable options.